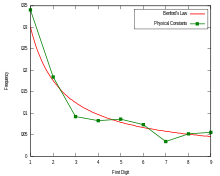
BENFORD'S LAW

I recently stumbled on a Netflix documentary that made my brain do summersaults. The program is called Connected and although all six episodes of the series are interesting and well done, Episode 4 called Digits fascinated me.

It's about a mathematical principle called Benford's Law (see below). I'd never heard of it and was surprised to learn that it originated from a simple observation about a now obsolete 19th century reference book. 

The Law seems to apply to any big batch of numbers from the length of airline routes to friend counts on social media sites, from the weight of atoms to the number of passes in soccer before an interception takes place.

Really quite astounding. In fact, its all pervasiveness in data sets gives credence to the belief that there's an underlying mathematical principle unifying everything in the universe. 

Conversely, and just as interesting, is the observation that when data sets don't follow Bedford's Law, it has likely been manipulated to deceive or misguide. 

Do watch the episode. Even if you're not a math nerd like me, I think you'll enjoy it..

  

The distribution of first digits, according to Benford's law. Each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit.

Frequency of first significant digit of physical constants plotted against Benford's law

Benford's law, also called the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation about the frequency distribution of leading digits in many real-life sets of numerical data. The law states that in many naturally occurring collections of numbers, the leading digit is likely to be small.^[1] For example, in sets that obey the law, the number 1 appears as the leading significant digit about 30% of the time, while 9 appears as the leading significant digit less than 5% of the time. If the digits were distributed uniformly, they would each occur about 11.1% of the time.^[2] Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.

It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, house prices, population numbers, death rates, lengths of rivers, and physical and mathematical constants.^[5] Like other general principles about natural data—for example the fact that many data sets are well approximated by a normal distribution—there are illustrative examples and explanations that cover many of the cases where Benford's law applies, though there are many other cases where Benford's law applies that resist a simple explanation.^[6] It tends to be most accurate when values are distributed across multiple orders of magnitude, especially if the process generating the numbers is described by a power law (which are common in nature).

The law is named after physicist Frank Benford, who stated it in 1938 in a paper titled "The Law of Anomalous Numbers",^[7] although it had been previously stated by Simon Newcomb in 1881.^[8][9]

• •